the intuition of log returns
when you do anything with data, you should think about the intuition of each thing you do, and what it represents "in the real world".
let's take the example of log returns, which some people tell me they find confusing.
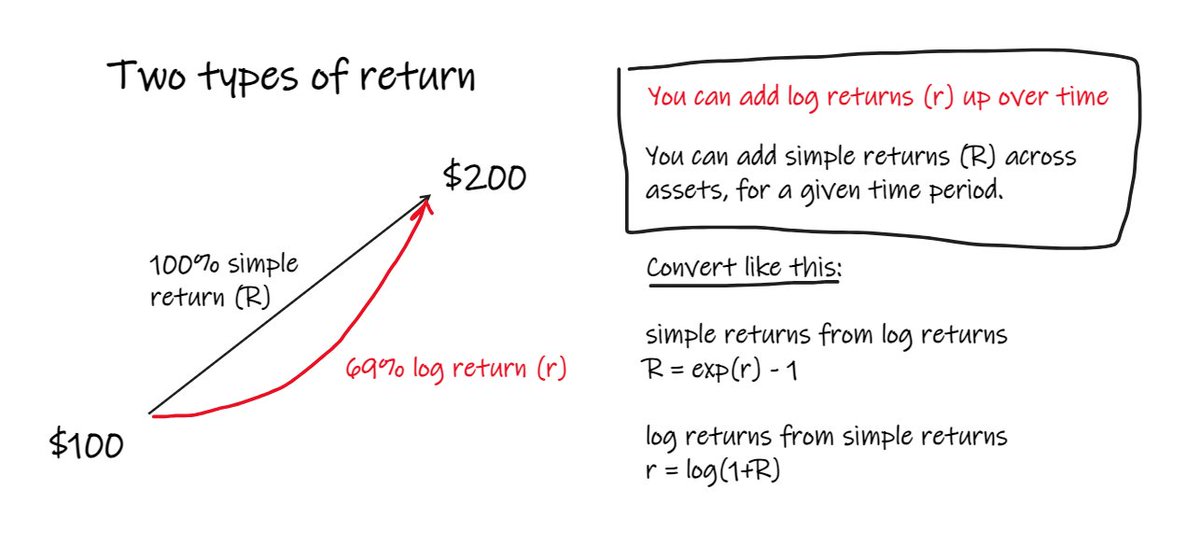
consider an asset whose price goes from $100 to $200
assume there are no other cashflows like dividends associated with this thing.
what are the returns for being long?
the intuitively obvious answer is 100%
it went up $100, the same as its price at the start of the period.
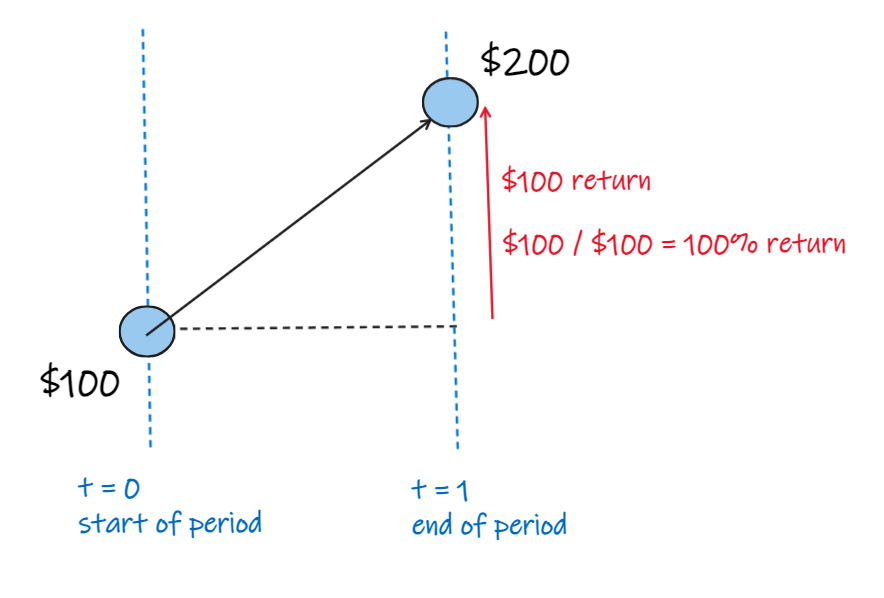
but let's be careful we understand what that represents.
that represents the return:
- over the whole period
- calculated on the initial value at the start of the period
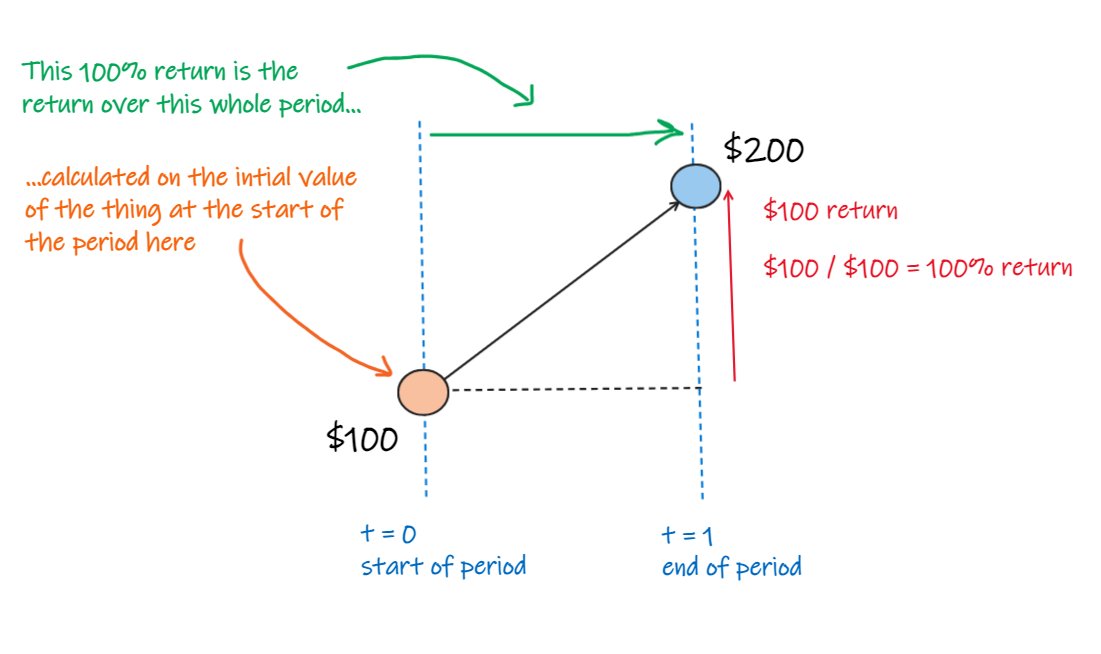
to be tediously clear...
- the asset is worth $100 at the start
- it increased $100
- so the total return over the period, on the initial value, is 100%.
we might call this the periodic arithmetic return. or simple return.
now let's consider log returns.
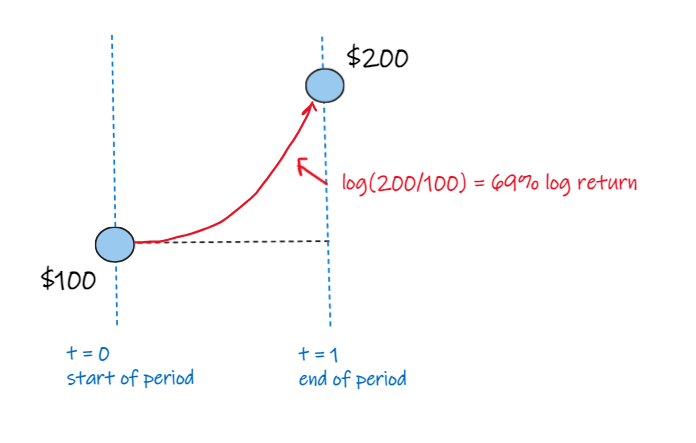
we calculate log returns for this period as log(200/100) = 69%
that's lower.
what does it represent?
it represents the return that we'd apply continuously throughout the period (rather than to the price at the start) to get to the end price.
i told you the answer, but if it's your first time thinking about this seriously, that probably won't have made any sense.
so let's go through it slow.
it's obvious that 69% isn't the return over the period on the initial value, because that would only get us to $169, not $200
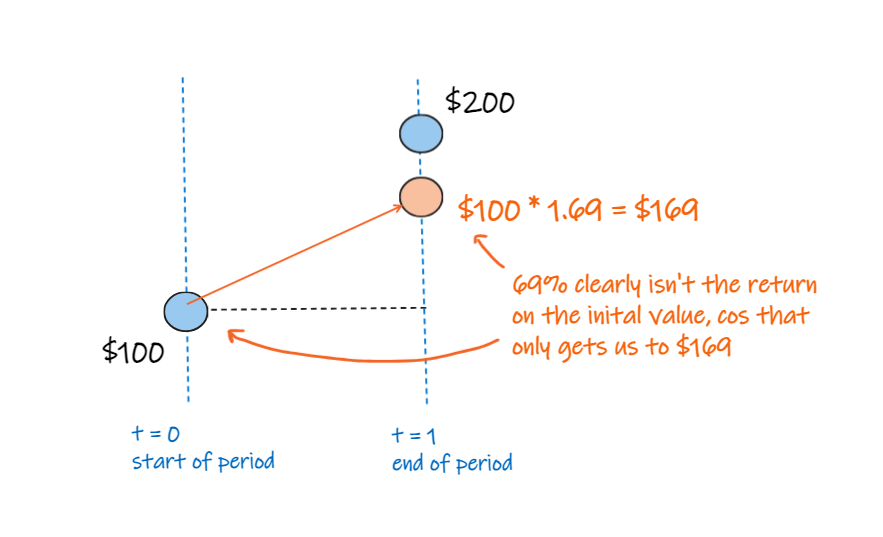
now let's split our period into two.
we'll apply a return of 69% / 2 to the first period, to get $135.
then apply a return of 69% / 2 to $135, to end up at $181.
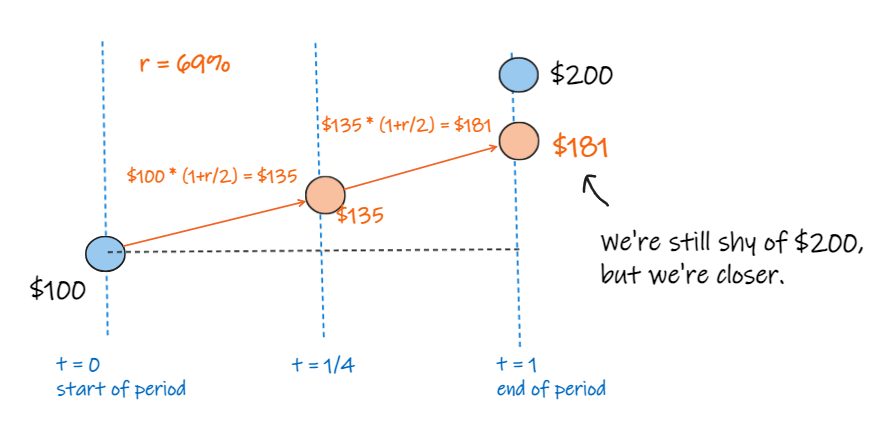
which still isn't $200, but is closer.
now, let's split our period in four.
and apply a return calc of 69% / 4 to each of the four periods.
now we end up at $190
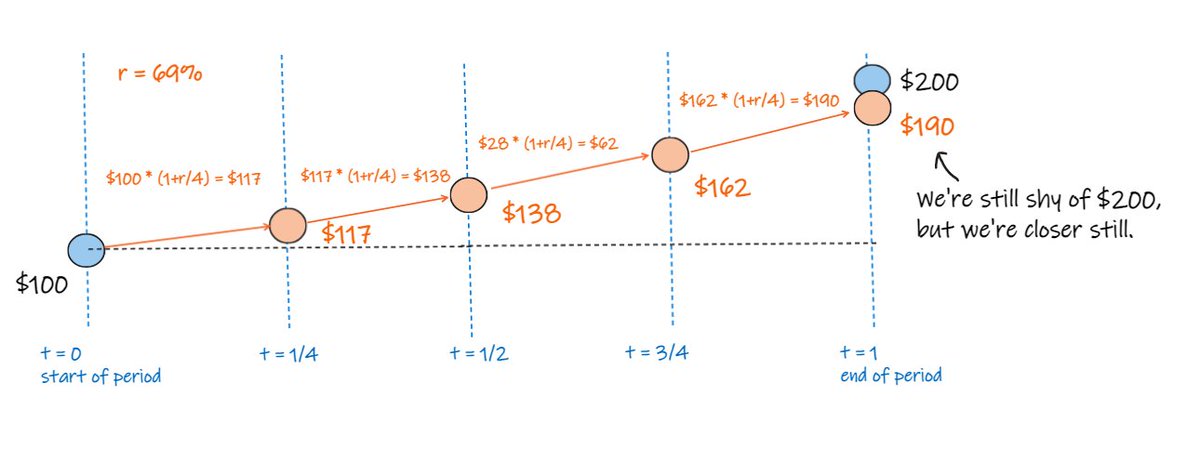
which still isn't $200, but is closer still.
now, split the period in eight equal periods.
and apply a return calc of 69% / 8 to each of the eight periods.
now we end up at $194, which is closer still...
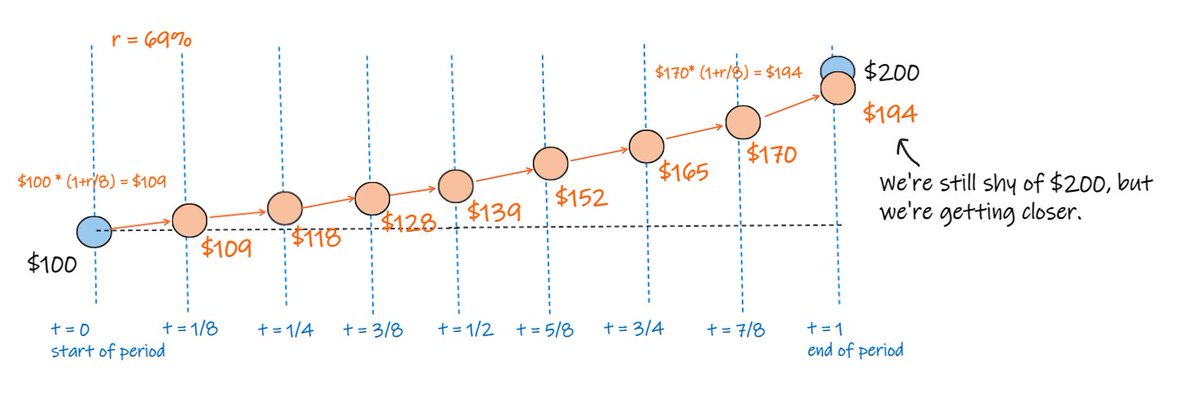
now we split it into thirty two equal periods
we apply a return calc of 69% / 32 to each of the 32 periods.
now we end up at $199, which is really close.
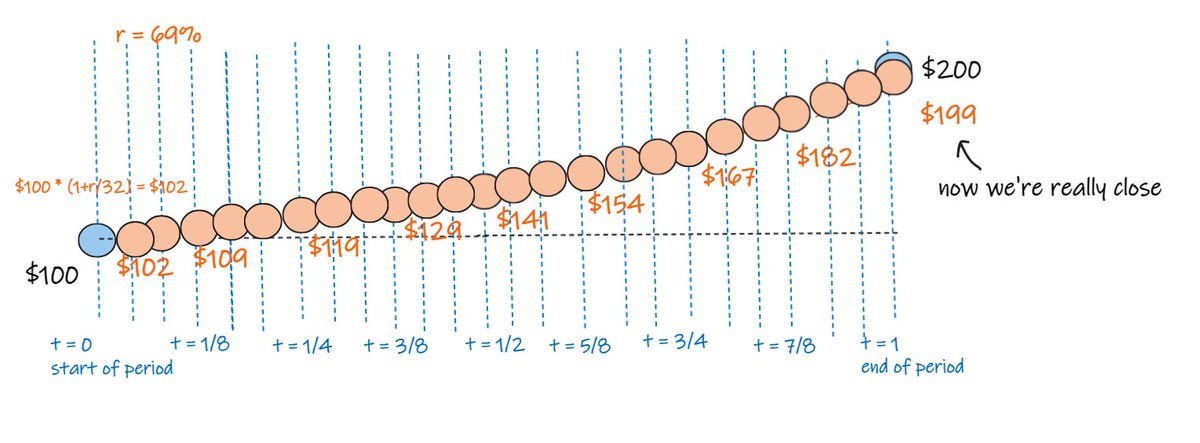
i won't draw this, but if we divide it into 64 periods we end up at $199.30
and if we do this with 200 periods we end up at $199.76
and if we do it over an infinite number of tiny periods we get to exactly $200.00.
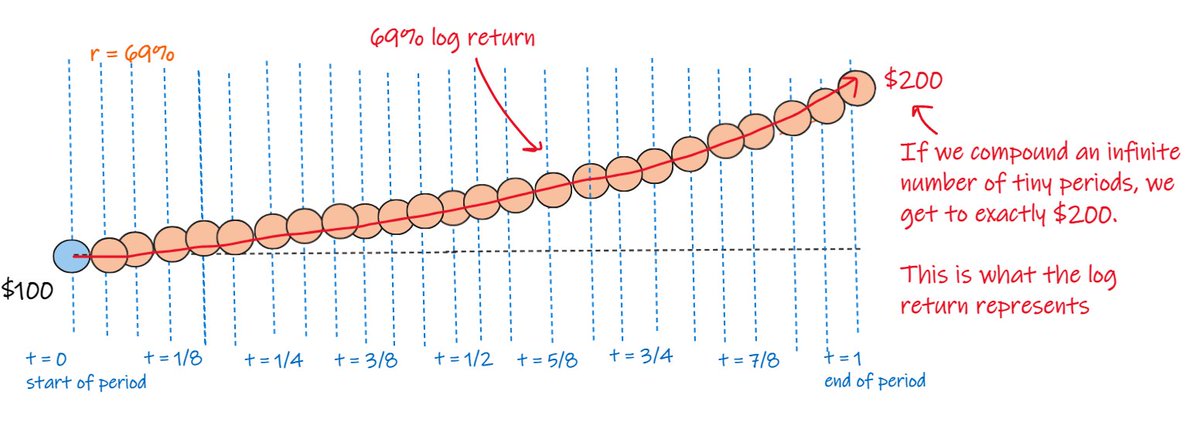
this is what the log return represents.
they're useful cos:
- you can add them up over time
- they're easy to compare over different time periods of different lengths cos they scale linearly
- you can easily convert them into simple returns and back (see image at the top)
- they're symmetrical on the upside and downside (if you make 10% and lose 10% you end up at the same place.)
beep...boop.